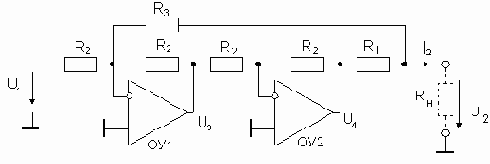
Источник тока, управляемый напряжением, для заземленной нагрузки
Для определения выходного тока источника запишем уравнения по первому закону Кирхгофа для n- и р-входов и выхода операционного усилителя:
(Uвых – Un)/R2 – Un/R3 = 0,
(U1 – Up)/R2 + (U2 – Up)/R2 = 0,
(Uвых – U2)/R1 – (U2 – Up)/R2 – I2 = 0. /p>
Из этих уравнений с учетом того, что Un=Up, получим:
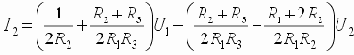
Приравняв нулю коэффициент при U2, найдем условие независимости выходного тока от напряжения на нагрузке –
| R3 =(R2)2/(R1 + R2). | (8) |
Теперь выражение для выходного тока источника будет иметь вид:
I2= U1/ (R1||R2).
Выполняя точную подстройку R3, можно добиться бесконечного выходного сопротивления источника тока на низких частотах при реальных характеристиках операционного усилителя. Недостаток схемы, однако, состоит в том, что внутреннее сопротивление Rи управляющего источника напряжения U1 входит в выражение (8) (оно добавляется к сопротивлению резистора, подключенного ко входу схемы). К тому же, ток управляющего источника напряжения зависит от сопротивления нагрузки. В результате полная балансировка источника невозможна, если Rи , как, например, у стабилитронов, зависит от тока.
Этого недостатка не имеет схема, приведенная на рис. 10. Здесь входной резистор присоединен к виртуальному нулю. Другое достоинство этой схемы состоит в отсутствии синфазного сигнала. Для расчета выходного тока в этой схеме используем следующее соотношение:
U4 = – U3 = U1 + (R2/R3) U2 .
Запишем уравнение по первому закону Кирхгофа для выхода схемы.