RC-генератор синусоидальных колебаний
В качестве звена обратной связи использован полосовой RC-фильтр, частотные характеристики которого приведены на рис. 37б. Здесь по оси абцисс отложена относительная частота W = wRC, поэтому средняя частота равна единице. Фазовый сдвиг на средней частоте y(1)=0. Следовательно, для выполнения условия баланса фаз выход звена обратной связи должен быть подключен к неинвертирующему входу ОУ. Коэффициент усиления полосового фильтра на средней частоте |b(1)|=1/3. Для выполнения условия баланса амплитуд ОУ по неинвертирующему входу должен иметь коэффициент усиления К=3. Поэтому
| R1=2R2 | (43) |
В целом, цепь, подключенная к ОУ (полосовой фильтр и делитель R1R2), называется мостом Вина-Робинсона.
При строгом выполнении условия (43) и идеальном ОУ в схеме на рис. 37а будут существовать незатухающие колебания с частотой f=1/2pRC.Однако амплитуда этих колебаний не будет определена. Кроме того, даже самое незначительное уменьшение R1 по сравнению с (43) вызовет затухание колебаний. Напротив, увеличение R1 по сравнению с (43) приведет к нарастанию амплитуды колебаний вплоть до насыщения усилителя и, как следствие, к появлению заметных нелинейных искажений формы кривой выходного напряжения генератора. Эти обстоятельства требуют использования в составе генератора системы автоматического регулирования амплитуды. В простейшем случае для этого в качестве резистора R2 используют нелинейный элемент – микромощную лампу накаливания, динамическое сопротивление которой с ростом амплитуды тока увеличивается.
Низкочастотные синусоидальные колебания могут быть также получены путем моделирования дифференциального уравнения синусоидальных колебаний с помощью операционных усилителей. Схема, реализующая этот метод, подобна схеме фильтра второго порядка, построенного на основе метода переменных состояния, приведенной на рис. 21. Эта схема, как и предыдущая, требует применения системы автоматического регулирования амплитуды колебаний.
Сложность обеспечения высокой стабильности амплитуды колебаний при минимальных искажениях выходной синусоиды существенно усложняет построение генераторов синусоидальных колебаний и управление ими. Лучшие результаты во многих случаях, особенно на низких и инфранизких частотах, дает применение так называемых функциональных генераторов.
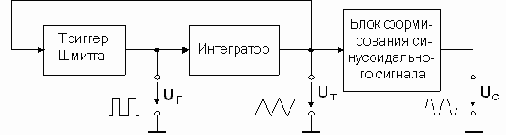
Блок-схема простейшего функционального генератора приведена на рис. 38. Он включает генератор прямоугольного и треугольного напряжения и блок формирования синусоидального сигнала.